"Imagination is more important than knowledge. Knowledge is limited. Imagination encircles the world." Einstein

Support Vector Machine

SVM is an alternative view for logistic regression. Starting from logistic regression we can derive a good understanding of basic SVM.

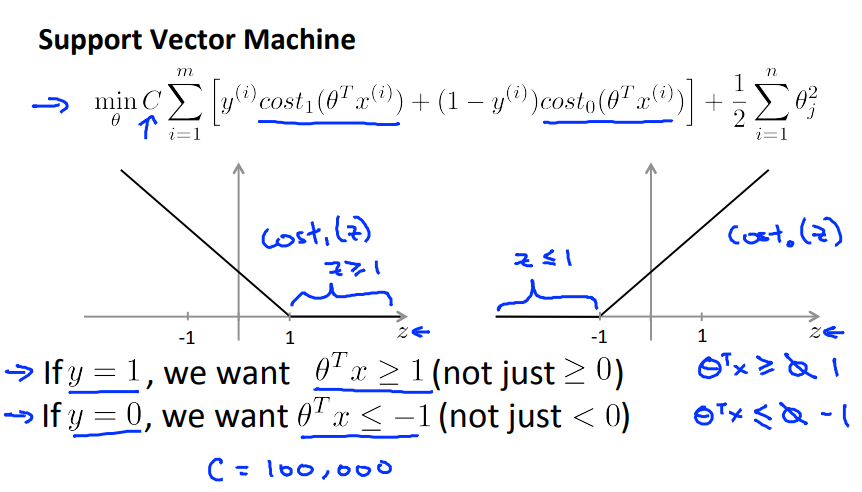
Also helpfull is the concept of large margins or decision boundaries to help understand what SVM’s are doing under the hood.

SVM Decision Boundary

$min\, C \sum_{i=1}^{m}\left[ y^{(i)} cost_1(\theta^T x^{(i)}) + (1-y^{(i)} cost_0(\theta^T x^{(i)})\right] + \frac{1}{2}\sum_{i=1}^n \theta_j^2$

Kernels

###But How To Get Those Landmarks? The training example are exactly the landmarks with the corresponding values (0 or 1) to which category they belong to.

Given example x:
$f_1 = similarity(x,l^{(1)})$
$f_2 = similarity(x,l^{(2)})$
…

In a Gaussian Kernel similarity corresponds to: $exp\left(-\frac{\Vert x - l^{(i)}\Vert^2}{2\sigma^2}\right)$

All the $f_{(i)}$ are grouped for each training example $(x^{(i)}, y^{(i)})$ in a feature vector $f^{(i)}$ with the first entry $f_0^{(i)} = 1$.

Hypothesis:
Given $x$, compute features $f \in \mathbb{R}^{m+1}$
Predict $y=1$ if $\theta^{T}f \ge 0$

Training:
$min\, C \sum_{i=1}^{m}\left[ y^{(i)} cost_1(\theta^T f^{(i)}) + (1-y^{(i)} cost_0(\theta^T f^{(i)})\right] + \frac{1}{2}\sum_{i=1}^n \theta_j^2$

By solving this minimization problem, we get our parameters for the support vector machine.

Implementation Detail

The last parameter is usually implemented as $\theta^T\theta$, while ignoring $\theta_0$. This also corresponds to $\Vert \theta \Vert^2$. This is done due to large numbers of features n, to reduce its computation time.

SVM Parameters

$C = \frac{1}{\lambda}$.

• Large C: Lower bias, high variance.
• Small C: Higher bias, low variance.

$\sigma^2$

• Large $\sigma^2$: Features $f_i$ vary more smoothly. Higher bias, lower variance.
• Small $\sigma^2$: Features $f_i$ vary less smoothly. Lower bias, high variance.

SVM Software Packages

• liblinear
• libsvm

If we use existing SVM’s we have to specify:

• Choice of parameter C
• Choice of kernel (similarity function), eg. no kernel means linear kernel and it predicts $y = 1$ if $\theta^Tx \ge 0$.

In many frameworks we have to define the Kernel function, e.g. in Octave/Matlab And note, that we do perform feature scaling before using the Gaussian kernel.

All valid similarity functions used in kernels have to satisfy the technical condition called Mercer’s Theorem.

Off-The-Shell Kernels

• Polynomial kernel $k(x,l) = (x^T l + constant)^{degree}$
• String kernel
• Chi-square kernel
• Histogram intersection kernel

Multi-Class Classification

Many SVM packages already have built-in multi-class classification functionalty.