"Try not to become a man of success, but rather try to become a man of value." Einstein

Example: Predicting Movie Ratings

• User rates movies using zero to five stars
• 5x movies and 4x persons
• $n_u$ is no. of users
• $n_m$ is no. of movies
• $r(i,j)$ is 1 if user j has rated movie i
• $y^{(i,j)}$ is rating given by user j to movie i (defined only r(i,j) = 1)

Content Based Recommendations

Problem Formulation

$r(i,j)$ is 1 if user j has rated movie i
$y^{(i,j)}$ is rating given by user j to movie i
$\theta^{(i)}$ = parameter vector for user j
$x^{(i)}$ = feature vector for movie i For user j, movie i, predicted rating: $(\theta^{(j)})^T \cdot (x^{(i)})$

$m^{(j)}$ = no. of movies rated by user j

To learn $\theta^{(j)}$: Use linear regression with some simplifications

Collaborative Filtering

We have no information about the classification of our movies. So what do we do? How to we calculate $\theta^{(j)}$?

From the data of our user we can get the parameters for the $\theta$ vectors.

Learn The Feature Vector x

Given $\theta^{(1)},...,\theta^{(n_u)}$ to learn $x^{(1)},..., x^{(n_m)}$

How To Solve The Chicken Or Egg Problem

Both $x^{(i)}$ and $\theta^{(i)}$ can be extracted from the data set. Guess $\theta \to x \to \theta \to x \to ...$

This going back and forth to estimate the two parameters is not the fastest approach. There are also others as the proposed simultanous approach:

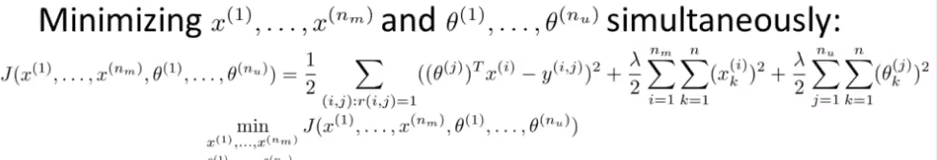
The above shown cost function for the collaborative filtering looks like this. This one contains the regularization term. Be aware of only using elements (movies) to sum up for the cost function which have been rated by a user. The same has to be done for the calculation of the gradients!

% Multiply the squared body of the function
%  by the matrix containing the values R_ij,
%  where R_ij = 1 if i-th movie was rated by
%  the j-th user
J = (1/2) * sum(sum(R .* SquardBody));

How To Apply The Algorithm

% For every feature vector x_i calulate the following gradient
X_grad(i,:) = (X(i,:) * Theta_tmp' - Y_tmp) .* Theta_tmp;

Vectorized Approach

% Calculating the gradient for all feature vectors
% Notes: X - num_movies  x num_features matrix of movie features
%   Theta - num_users  x num_features matrix of user features
%   Y - num_movies x num_users matrix of user ratings of movies
%   R - num_movies x num_users matrix, where R(i, j) = 1 if the 
%      i-th movie was rated by the j-th user
X_grad = (R .* ((X * Theta') - Y)) * Theta; 
Theta_grad = (R .* ((X * Theta') - Y))' * X;

Low Rank Matrix Factorization

Stacking all movie ratings into matrix X with each movie per row (transposed) and all user ratings into matrix $\theta$ with each user per row (transposed), the resulting matrix is called a Low Rank Matrix.

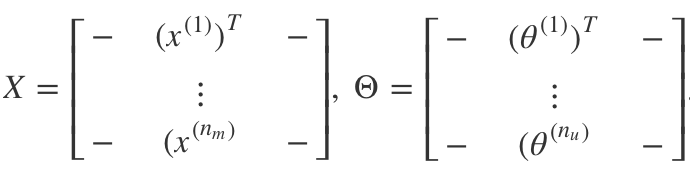
Finding a Feature Vector

For each product i, we learn a feature vector $x^{(i)} \in \mathbb{R}^n$.

How to find movies j related to movie i ?
5 most similiar movies to movie i :
Find the 5 movies j with the smallest $\Vert x^{(i)} - x^{(j)}\Vert$.

Mean Normalization

What if a user has not rated any movies? The first term in the minimization algorithm therefore doesn’t play any role and the $\theta^{(5)}$ is a zero vector for this user.

BUT this above described approach doesn’t seem to be a good way…

We should apply a mean normalization to get the initial ratings for a user without any ratings: