"It’s not that I’m so smart, it’s just that I stay with problems longer." Einstein

Key Components Of Autonomous Flight

• State Estimation
• Control
• Mapping
• Planning

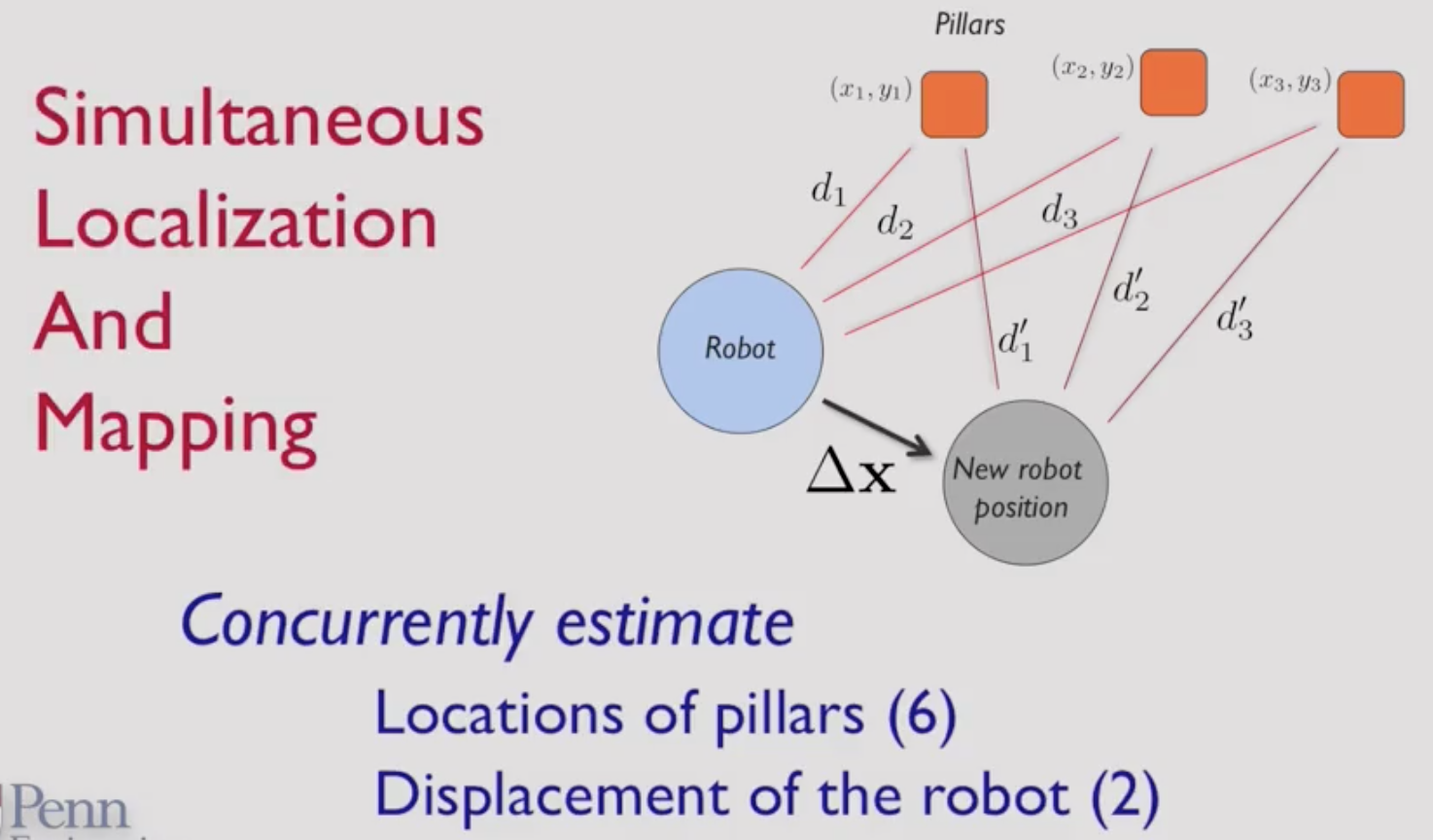
State Estimation

SLAM = Simultaneous Localization And Mapping

Dynamical Systems

Systems where the effects of actions do not occur immediately. Every dynamical system is defined by its states: a collection of vairables that completely characterizes the motion of a system. Evoluton of these states over time is often given by a set of governing ordinary differential equations.

• Example 1: Mass-Spring System $m\ddot{y}(t) + ky(t) = u(t)$
• Example 2: Quadrotor (facilitate)

Control Of Height

$\sum_{i=1}^4 k_F\omega_i^2 + mg = ma$
where $a = \frac{d^2x}{dt^2} = \ddot{x}$
becomes: $u = \frac{1}{m} \left[ \sum_{i=1}^4 k_F\omega_i^2 + mg\right]$ where second order dynamic system $u =\ddot{x}$

Control Of A Linear Second-Order System

Problem

Find a control input function $u(t)$ so that $x(t)$ follows the desired trajectory $x^{des}(t)$

General Approach

Define error $e^{(t)} = x^{des}(t) - x(t)$
We want $e(t)$ to converge exponentially to zero

Strategy

Find $u(t)$ such that
$\ddot{e} + K_v \dot{e} + K_pe = 0$
where $K_p, K_v > 0$
and $K_v$ is the Derivative Gain
and $K_p$ is the Proportional Gain

Proportional-Derivative Controller (PD)

$u(t) = \ddot{x}^{des}(t) + K_v \dot{e}(t) + K_p e(t)$

• Proportional control acts like a spring (capacitance) response
• Derivative control is a viscous dashpot (resistance) response
• Large derivative gain makes the system overdamped and the system converges slowly

The dynamic equation for the motion of the quadrotor in the $z$ direction is
$\ddot{z} = \frac{u}{m} - g$

Let us solve this for $u$, replace $z$ and calculate the error $e$ as indicated above resuts in:

$u = m(\ddot{z}_{des} + K_pe + K_v\dot{e} + g)$

Proportional-Integral-Derivative Controller (PID)

In the presence of disturbances (e.g. wind) or modeling errors (e.g. unkown mass), it is often advantageous to use PID control:

$u(t) = \ddot{x}^{des}(t) + K_v \dot{e}(t) + K_p e(t) + K_i \int_0^t e(\tau)d\tau$

PID control generates a third-order closed-loop system. Integral control makes the steady-state error go to zero.

Agility And Maneuverability

Let’s look at the situation from Maximum Velocity to Rest. Max deceleration is achieved by tilting the robot. But in this case the robot will also lose height.

Agility

Two key ideas:

• Accelerate quickly by maximizing $a_{max}$
  $\text{maximize}\frac{u_{1,max}}{W}$
• Roll/Pitch quickly by maximizing $\alpha_{max}$
  $\text{maximize}\frac{u_{2,max}}{I_{xx}}$

Effects Of Size

• Froude scaling
  $v \sim \sqrt{l}$
  $F \sim l^3$
  $a \sim 1, \alpha \sim \frac{1}{l}$
• Mach scaling
  $v \sim 1$
  $F \sim l^2$
  $a \sim \frac{1}{l}, \alpha \sim \frac{l}{l^2}$

Quadrotor Kinematics

Properties Of Rotation Matrix

• Orthogonal
  • Matrix times its transpose equals the identity
• Special orthogonal
  • Determinant is +1
• Closed under multiplication
  • Product of any two rotation matrices is another rotation matrix
• Inverse of a rotation matrix is also a rotation matrix

Rotations

Euler Angles

Euler angles are a composition of three rotations. Any rotation can be described by three successive rotations about linearly independent axes. This is only an almost 1-1 transformation.

Axis/Angle Representations For Rotations

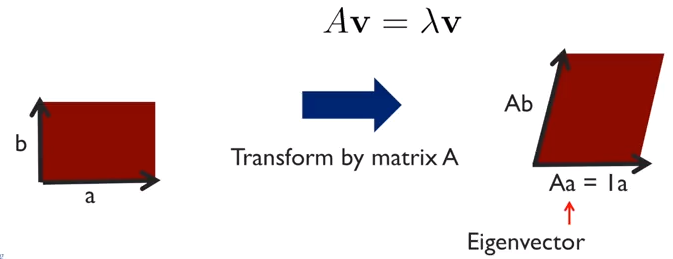
Eigenvalues And Eigenvectors

• Determinant is a scalar property of square matrices, denoted $det(A)$ or $\vert A\vert$
  
  • Think of rows of an $x \times x$ matrix as n vectors in $\mathbb{R}^n$.
    
  • The determinant represents the space contained by these vectors

The determinant of a 2x2 matrix represents the aera of the parallelogram. Likewise, the determinant of a 3x3 matrix is the volume of the cube.

Definition

Eigenvectors are vectors associated by a squared matrix that do not change in direction when multiplied by the matrix.

Eigenvalues are scalar values representing how much each eigenvector changes in length.

$A\mathbf{v} = \lambda \mathbf{v}$

Finding Eigenvalues

1. Calculate $det(A - \lambda \mathbf{I})$
   
2. Find solutions to $det(aA - \lambda \mathbf{I})=0$
   

There will be n eigenvalues for an n x n matrix, but not all of them have to be distinct or real values.

Finding Eigenvectors

1. For each eigenvalue, solve the equation $A\mathbf{v} = \lambda \mathbf{v}$
   or $(A-\lambda\mathbf{I})\mathbf{v} = 0$
   

There will be at least one eigenvector for each eigenvalues. if some eigenvalues are repeated, there might be an infinite number of eigenvectors for that eigenvalue.

Axis/Angle to Rotation Matrix

Rotation of a generic vector p about u through $\phi$

$Rp = p \cos\phi + uu^T \, (1-\cos\phi)p + \hat{u}p \sin \phi$
where $\hat{u}$ is a skew-symmetric matrix or $u\times$.

A skew-symmetric matrix is a matrix where $\mathbf{A}^T = -A$

$\left(\begin{matrix} 0 & -A_{21} & A_{13} \\ A_{21} & 0 & -A_{32} \\ -A_{13} & A_{32} & 0 \\ \end{matrix}\right)$

We can concisely represent a skew-symmetric matrix as a 3x1 vector:

$a = \left[\begin{matrix} A_{32} \\ A_{13} \\ A_{21} \\ \end{matrix}\right] = \left[\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \\ \end{matrix}\right]$

The hat operator is commonly used to seitch between these two representations.

Further is the hat operator also used to denote the cross product between two vectors. $\mathbf{u} \times \mathbf{v} = \mathbf{\hat{u}v}$

Let’s go back to our last formula: $Rp = p \cos\phi + uu^T \, (1-\cos\phi)p + \hat{u}p \sin \phi$

Removing the vector p from both sides results in the rotation matrix. $\text{Rot}(u, \phi) = I\cos\phi + uu^T(1-\cos\phi) + \hat{u}\sin\phi$

where $u$ is the axis of rotation and $\phi$ the rotation angle.

Rodrigue’s Rotation formula is:

1. (axis, angle) to rotation matrix map is many to 1
2. restricting angle to the intervall $[0,\pi]$ makes it 1-1, except for special cases
   $\phi = 0 \to \text{no unique axis}$
   $\phi = \pi \to u \text{or} -u \,\text{both axis}$
   

Quaternion

Quaternion is defined as: $q = (q_0, q_1, q_2, q_3)$
This can be interpreted as a constant + vector: $q = (q_0,\mathbf{q})$

Operations

Addition: $p \pm q = (p_0 \pm q_0, \mathbf{p} \pm \mathbf{q})$
Multiplication: $pq = (p_0q_0 - \mathbf{p}^T\mathbf{q}, p_0\mathbf{q} + q_0\mathbf{p} + \mathbf{p} \times \mathbf{q})$
Inverse: $q^{-1} = (q_0, -\mathbf{q})$

Vector Rotation With Quaternions

To rotate a vector p in $\mathbb{R}^3$ by the quaternion q:

1. Define quaternion:
   $p = (0,\mathbf{p})$
   
2. The result after rotation is:
   $p' = qpq^{-1} = (0, \mathbb{p}')$
   

We can easily compose two rotations: $q = q_2q_1$

Angular Velocity

$R^TR \to \text{Derivation} \to \dot{R}^TR + R^T\dot{R} = 0$>br>

Due to the fact that the rotation matrix is screw-symmetric we can think in terms of derivatives not of matrices instead of the corresponding vectors.

Mathematical Explanation

Mathematical Transformation

The velocity $\dot{g}$ in the inertial frame can be written as:
$\dot{q} = \dot{R}p$
This can be transformed by the multiplicating both sides with $R^T$. With this we get a better known form of the equation:
$R^T\dot{q} = R^T\dot{R}p$
where $R^T\dot{R}$ is referred to by $\hat{\omega}^b$. This encodes the angular velocity in body-fixed frame

We can transform this into the velocity in inertial frame $\dot{q}$:
$\dot{q} = \dot{R}R^Tq$
where $\dot{R}R^T$ is referred to by $\hat{\omega}^s$. This encodes the angular velocity in inertial frame.

Example

Calculate the angular velocity for a rotation about the z-axis:

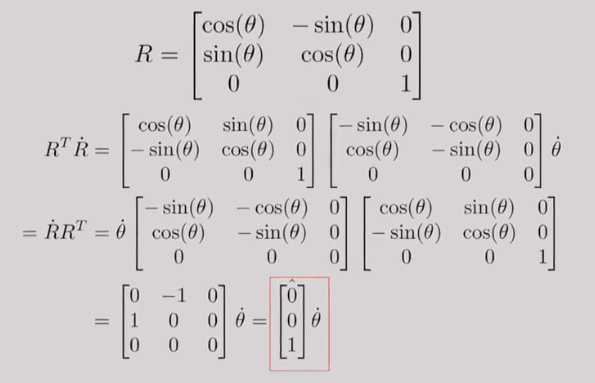
Quadrotor Dynamics

The here used and described equations of motions are the Newton and Euler Equations.

Newton-Euler Equations

We will use the Z-X-Y rotation convention. This means $\text{Yaw} \to \text{Roll} \to \text{Pitch}$

• Newton’s Equation of Motion for a Single Partile of mass m
  $\mathbf{F} = m\mathbf{a}$
  

System Of Particles

First we have to define the center of mass by
$\mathbf{r}_c = \frac{1}{m} \sum_{i=1,N} m_i\mathbf{p}_i$

The center of mass for a system of particles, S, accelerates in an inertial frame (A) as if it were a single particle with mass m (equal to the total mass of the system) acted upon by a force equal to the net external force.

Rate of change of linear momentum
$\mathbf{F} = \frac{^Ad\mathbf{L}}{dt} = \sum_{i=1}^{N}\mathbf{F}_i = m \frac{^Ad\,^A\mathbf{v}^c}{dt}$
with $\mathbf{L}$ as the linear momentum of the system of particles in the inertial frame A.

Rotational Equations

The rate of change of angular momemtumof the rigid body B relative to C in A is equal to the resultant moment of all external forces acting on the body relative to C:
$\mathbf{M}_C^B = \frac{^Ad\, ^A\mathbf{H}_C^B}{dt}$
with Angualr momemtum $\mathbf{H}$ of the rigid body B with the origin C in the inertial frame A

Angular momentum: $^A\mathbf{H}_C^B = \mathbf{I}_C \cdot ^A\omega^B$
with inerta tensor written as a 3x3 matrix with C as the origin.

Principal Axes and Principal Moments of Inertia

• Principal axis of inertia
  $u$ is a unit vector along a principal axis if $I \cdot u$ is parallel to $u$. There are 3 independent principal axes
• Principal moment of inertia The moment of inertia with respect to a principal axis, $u \cdot I \cdot u$, is called a principal moment of inertia.

Equations

How To Estimate These Parameters

State Vector:
$q = \left[\begin{matrix} x\\ y\\ z\\ \varphi\\ \theta\\ \psi\\ \end{matrix}\right], x = \left[\begin{matrix}q\\ \dot{q}\\ \end{matrix}\right]$

• q describes the configuration (position) of the system
• x descibesthe state of the system

Equilibrium at Hover:
$q_e = \left[\begin{matrix} x_e\\ y_e\\ z_e\\ 0\\ 0\\ \psi_e\\ \end{matrix}\right], x_e = \left[\begin{matrix}q_e\\ 0\\ \end{matrix}\right]$

• $q_e$ describes the equilibrium configuration of the system
• $x_e$ describes the equilibrium state of the system