"Imagination is more important than knowledge. Knowledge is limited. Imagination encircles the world." Einstein

Introduction

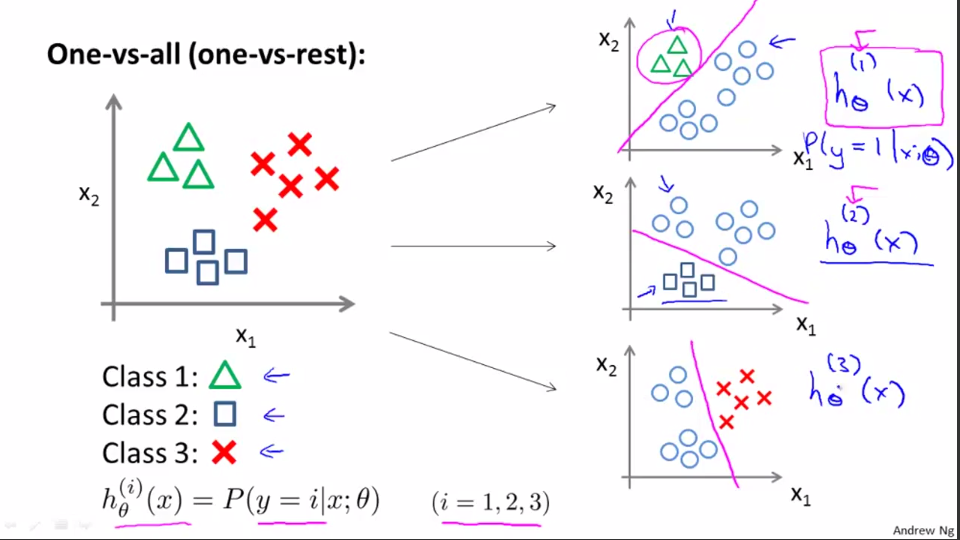
Multiclass Classification

One-vs-All

Problem of Overfitting

If we have too many features, the learned hypthesis may fit the training set very well ( $J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 = 0$ ), but fail to generalize to new examples (predict prices on new examples).

Adressing overfitting

Options:

1. Reduce number of features
   • Manually select which features to keep
   • Model selection algorithm
2. Regularization
   • Keep all the features, but reduce magnitude/values of parameters $\theta_j$.
   • Works well when we have a lot of features, each of which contributes a bit to predicting $y$.

The two terms of Bias and Variance are important for solving this issue.

Regularization

Small values for parameters $\theta_0$, $\theta_1$, …, $\theta_n$

• “simpler” hypothesis
• less prone to overfitting

Implementation

$J(\theta) = \frac{1}{2m} [ \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2 ]$

Regularized Logistic Regression

Recall that our cost function for logistic regression was: $J(\theta) = -\frac{1}{m}\, \sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)})) + (1-y^{(i)})log(1-h_{\theta}(y^{(i)}))]$
We can regularize this equation by adding a termn to the end: $J(\theta) = -\frac{1}{m}\, \sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)})) + (1-y^{(i)})log(1-h_{\theta}(y^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$
The second sum $\sum_{j=1}^n \theta_j^2$ means to explicitly exclude the bias term $\theta_0$. I.e. the $\theta$ vector is indexed from 0 to n (holding n+1 values, $\theta_0$ through $\theta_n$, by running from 1 to n, skipping 0. Thus, when computing the equation, we should continuously update the two following equations:

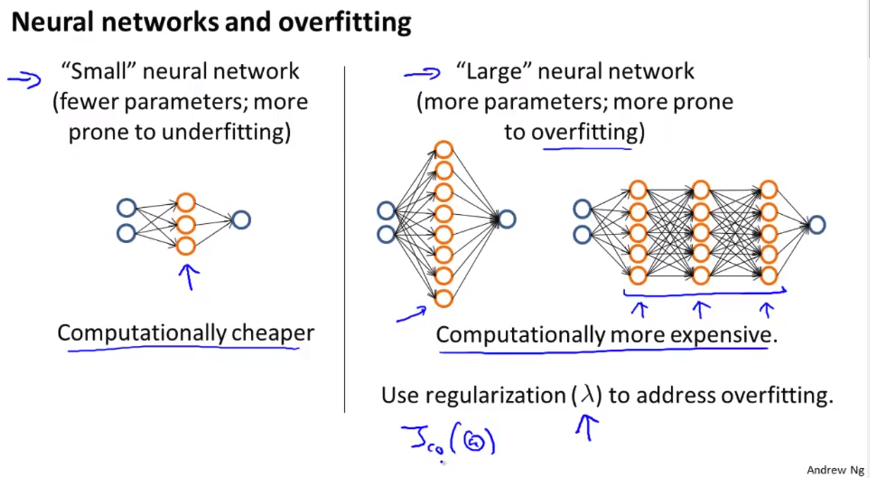
Neural Network

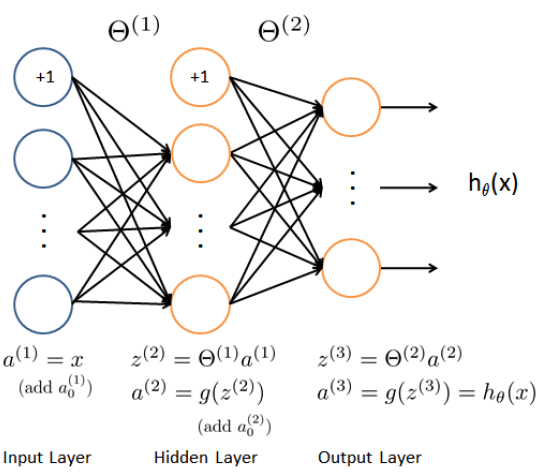
The image shows a simple neural network with one hidden layer. This is also the most reasonable default architecture, or if more than 1 hidden layer is used, they all have the some numbers of hidden units in every layer (usually the more the better).

The number of input units is related to the dimensions of features $x^{(i)}$. As well as the number of output units is related to the number of classes.

Training A Neural Network

1. Randomly initialize weights
2. Implement forward propagation to get $h_\Theta(x^{(i)})$ for any $x^{(i)}$
3. Implement code to compute cost function $J(\Theta)$
4. Implement backprop to compute partial derivates $\frac{\partial{}}{\partial{\Theta{jk}^{(l)}}}J(\Theta)$
5. Use gradient checking to compare $\frac{\partial{}}{\partial{\Theta{jk}^{(l)}}}J(\Theta)$ computed using backpropagation vs. using numerical estimate of gradient $J(\Theta)$. Then disable gradient checking code.
6. Use gradient descent or advanced optimization method with backpropagation to try to minimize $J(\Theta)$ as a function of parameters $\Theta$.

Debugging A Learning Algorithm

Suppose you have implemented regularized linear regression to predict something. However, when you test your hypothesis on a new set of houses, you find that it makes unacceptable large error in its predictions. What should we try next?

• Get more training examples
• Try smaller sets of features
• Try getting additional features
• Try adding polynomial features
• Try decreasing $\lambda$
• Try increasing $\lambda$

Machine Learning Diagostic

Diagnotis: A test that you can run to gain insight what is/isn’t working with a learning algorithm, and gain guidance as to how best to improve its performance.

Diagnostics can take time to implement, but doing so can be very good use of your time.

Model Selection

Split the data into three parts train, cross-validation and test data set. Now we use the cv set for model selection, the train set for training and the test set for validation.

Diagnosing Bias vs. Variance Problems

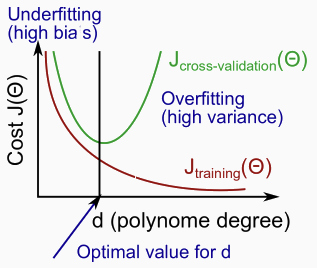
Combining With Regularization

What is the effect of regularization to the bias vs. variance problem?

Learning Curves

High Bias

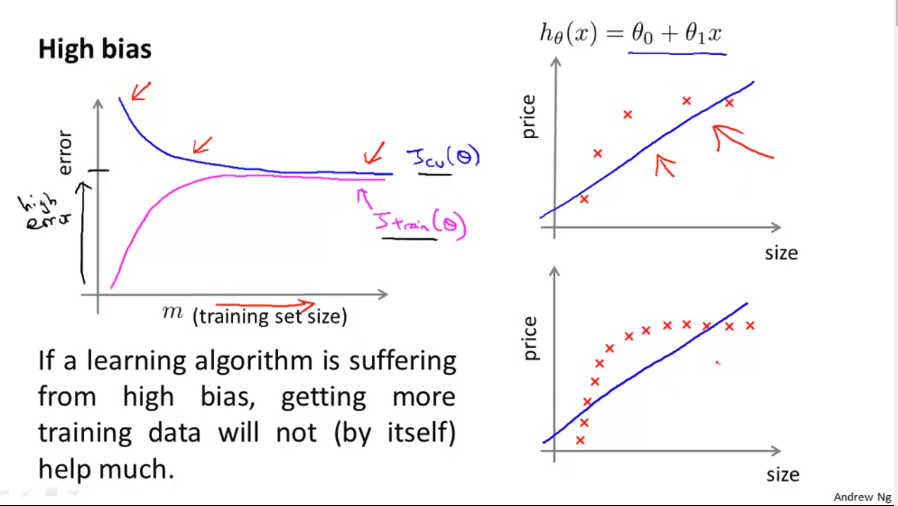
Learning curves can give us a feeling for the size of training data and the hypothesis we are choosing. At some point the bias remains at height even if we increase the training data set. For evaluation it is important that both errors are high.

High Variance

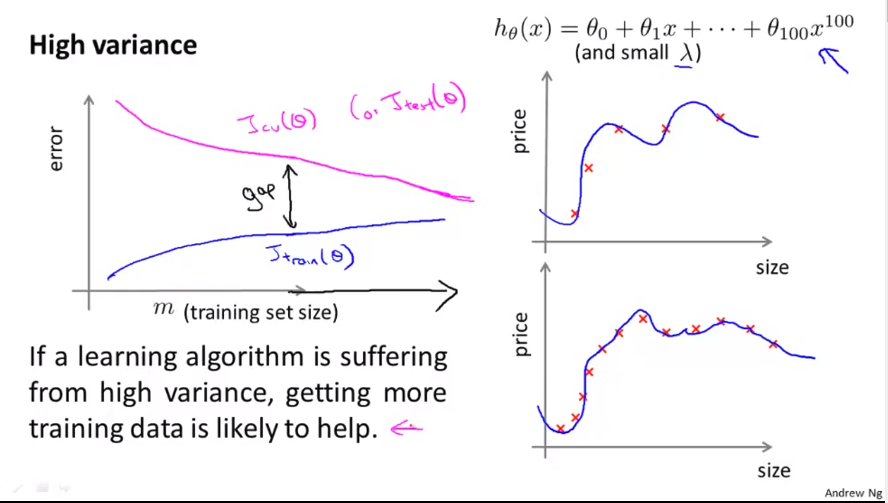
There is a similiar effect regarding high variance. An overfitted graph will get stuck with high error with the cross-validation set, BUT it will constantly but slowly reduce. And there increasing the data set helps to improve the hypothesis. For evaluation it is important that there is a gap between cross-validation and test error.

Debugging A Learning Algorithm

• Get more training examples $\to$ fixes high variance
• Try smaller sets of features $\to$ fixes high variance
• Try getting additional features $\to$ fixes high bias
• Try adding polynominal features $\to$ fixes high bias
• Try decreasing $\lambda$ $\to$ fixes high bias
• Try increasing $\lambda$ $\to$ fixes high variance

Error Analysis

Recommended Approach

• Start with a simple algorithm that you can implement quickly. Implement it and test it on your cross-validation data.
• Plot learning curves to decide if more data, more features, etc. are likely to help.
• Error analysis: Manually examine the examples(in cross validation set) that your algorith made errors on. See if you spot any systematic trend in what type of examples it is making errors on.

Precision And Recall

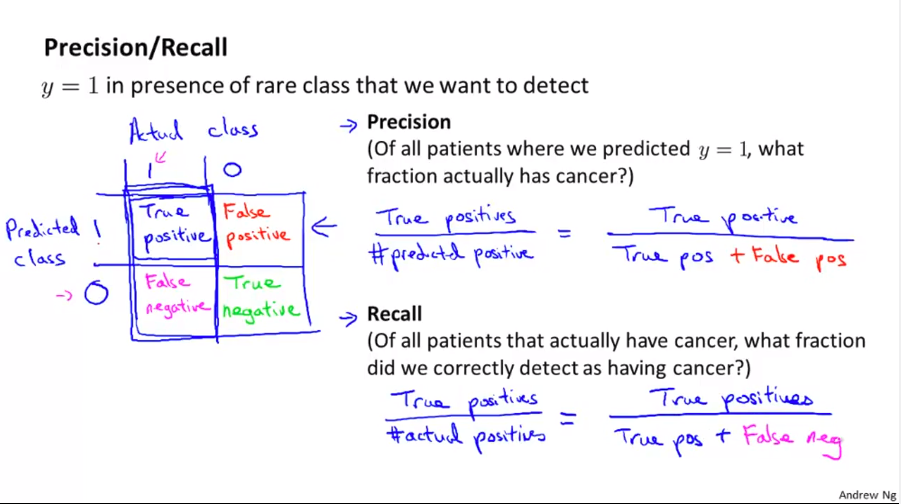
F1 Score

How can we compare precision and recall nubmers? A possibility is to take the average of those numbers. But this is not such a good solution, since extremas have a too big impact on the average.

$F_1$ Score $:= 2\frac{PR}{P+R}$

This $F_1$ Score can be used to define the threshold by applying it to the cross validation set.